[딥러닝] CNN 알고리즘의 원리
1. 서론
딥러닝 알고리즘 중 하나인 ‘CNN’에 대해 수학적, 공학적으로 분석해보고싶어졌다. 왜 이름이 CNN 인지? CNN의 핵심 수학 공식 ‘합성곱’이 무엇인지? CNN에 사용되는 알고리즘들은 어떠한 것들이 있는지? 등 입문자면 누구나 궁금해할만한 부분을 공부해보았다.
2. CNN 알고리즘이란
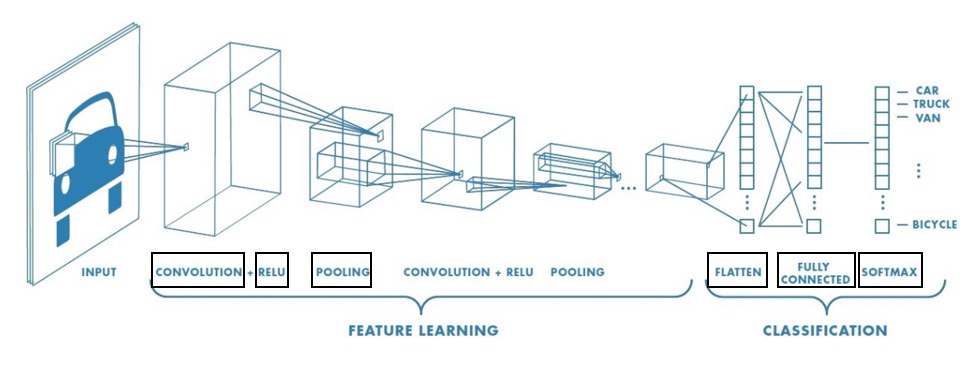
‘Convolution Neural Network’의 약자이다. 합성곱 신경망이라는 뜻이며 이미지 분류에 흔히 쓰인다. (ex. 고양이, 강아지, 토끼 등의 사진을 입력했을 때 이를 구분할 수 있도록) 전체적인 Flow는 다음 사진과 같다. 크게는 Input → Feature Learing → Classification 이렇게 세 단계로 구분되며 입문자가 봤을 때 생소한 단어는 검은색 네모로 표시해놓았다. 즉 우리가 공부해야되는 부분에 해당한다.
3. 합성곱(Convolution)이란
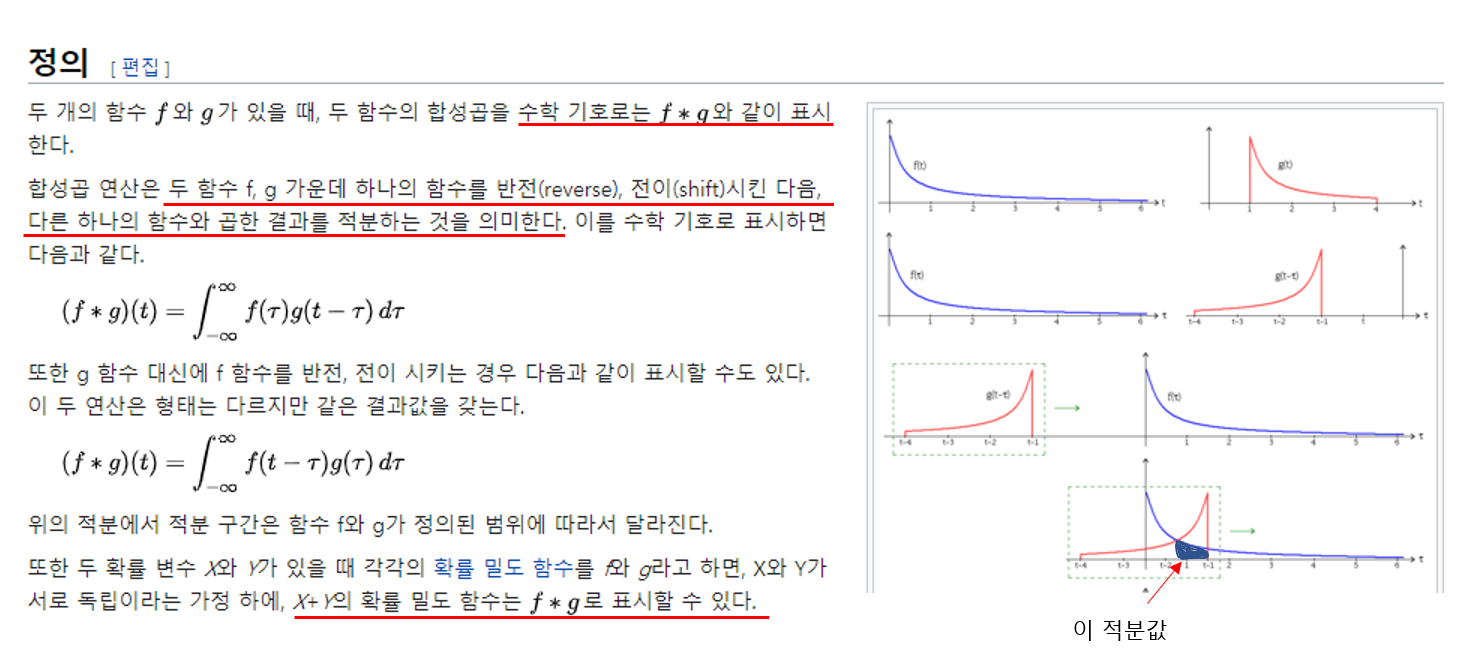
수학적인 정의는 다음 사진과 같다. 가장 와닿을 수 있게 이해하는 방법은 마지막 빨간 밑줄을 읽어보면 직관적으로 알 수 있다. 즉 f(a)라는 확률밀도함수와 g(b)라는 확률밀도함수가 있고 a, b가 서로 독립인 경우를 예를 들면 된다.
공식 유도를 위해 예시를 하나 들어보자. A주사위를 던졌을 때 특정 숫자가 나올 확률 f(a) 함수가 있다(a는 1이상 6이하). 그리고 B 주사위를 던졌을 때 특정 숫자가 나올 확률 g(b) 함수가 있다(b는 1이상 6이하). 이때 A와 B를 던져 나온 숫자의 합이 7일 확률을 구한다고 가정해보자. 계산식은 다음과 같다.
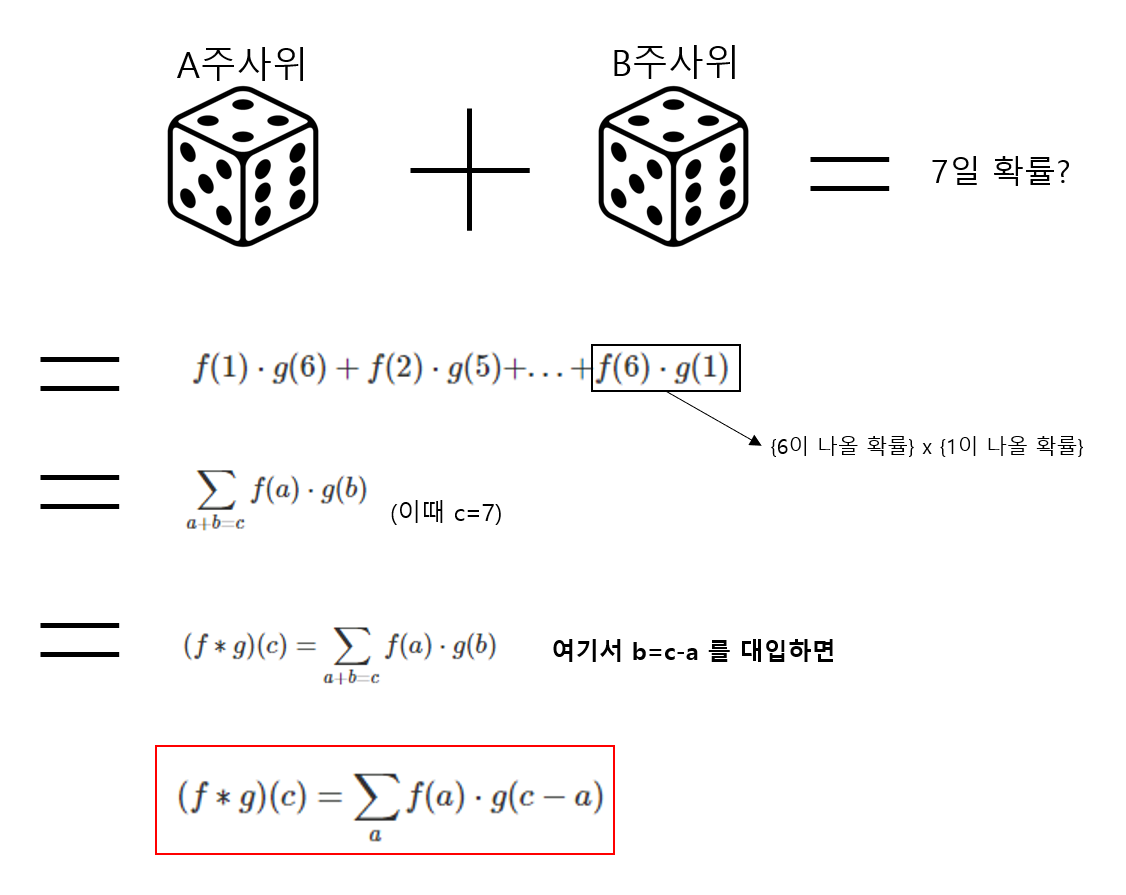
주사위 확률 예시는 정의역이 1, 2, 3, 4, 5, 6으로 구성된 이산함수이다. 위키백과에 기록된 ‘이산 합성곱’의 예시를 보면 내가 도출해낸 공식과 같다는 것을 알 수 있다.

4. CNN에서 사용되는 합성곱
A. filter 란?
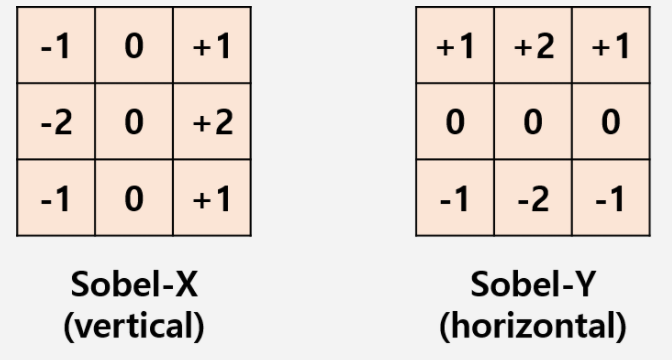
해당 내용을 설명하기에 앞서서, ‘필터’라는 개념에 대해 먼저 이해해야한다 (‘커널’이라고도 불린다). 문자 그대로 이해하면 편하다. 침고로 이제부터는 모든 함수나 입력값 등을 행렬로 생각해보자. 이미지도 행렬로 표현할 수 있다. 자주 쓰이는 필터는 다음 사진과 같은 2개의 3x3 행렬이다. 좌측 Sobel-X 필터는 수직으로 필터링되고, 우측 Sobel-Y 필터는 수평으로 필터링된다.
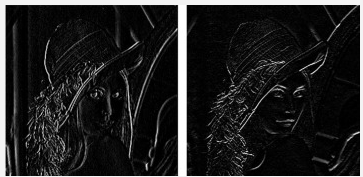
다음과 같은 여자 사진이 있다. 이 사진에 위에서 언급한 2개의 필터를 씌운다고 생각해보자.

다음 사진이 2개의 필터를 씌운 사진이다. (좌측이 Sobel-X, 우측이 Sobel-Y)
2개의 필터릉 사용한 사진을 합치면 다음과 같이 원본 사진의 feature를 확인할 수 있다.

filter란 이미지에서 특정 feature를 추출하기 위한 거름막이라고 생각하면 된다. 다음 카테고리에서 이것이 수학적으로 어떻게 계산되는지 알아보겠다.
(참고: 앞서 말했듯이 CNN은 이미지 분류에 특화되어있다. 이때 이미지의 Color에는 R,G,B에 대한 3개의 채널로 구성되는데 보통 연산량을 줄이기위해 색상 정보를 없애고 흑백으로 만들어 처리한다.)
B. CNN에서 사용되는 합성곱 (filter 이용하기)
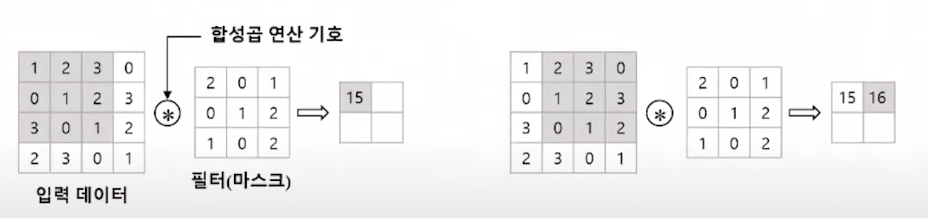
우리는 합성곱의 공식이 어떤지 확인하였다. 그럼 CNN에서 이를 어떻게 이용할까? 다음 사진과 같이 행렬을 통해 연산한다. 입력 데이터의 좌측 상단에서부터 우측 방향으로 필터에 해당하는 행렬크기(다음 예시에서는 3*3) 만큼 나눈 뒤 합성곱을 계산한다. 서로 대응하는 원소끼리 곱한 후 총합을 구하면 된다. 이러한 연산을 Fused Multiply-Add(FMA)라고 한다.
(1x2 + 2x0 + 3x1) + (0x0 + 1x1 + 2x2) + (3x1 + 0x0 + 1x2) = 15
(2x2 + 3x0 + 0x1) + (1x0 + 2x1 + 3x2) + (0x1 + 1x0 + 2x2) = 16
…
이때 필터가 움직이는 간격을 스트라이드(Stride)라고 부른다. 여기서는 스트라이드가 1인 경우이다.
이를 수식으로 나타내면 다음과 사진과 같다. (위에서 정리한 공식은 변수(주사위를 던져 나올 숫자)가 1개였지만 이미지의 경우 2차원 평면(높이, 너비)으로된 픽셀로 구성되어있어 변수의 개수가 다르다)
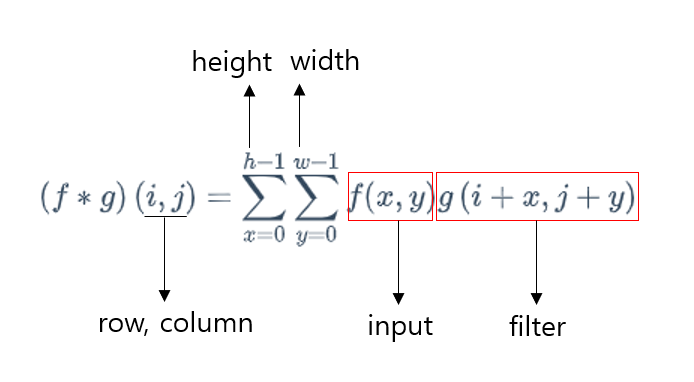
그런데 여기서 의문점이 생긴다. 위에서 도출해낸 ‘합성곱’ 공식에서는 g 함수의 인자에서 각각 x와 y를 빼야 정상이다. g(i-x, j-y) 처럼 말이다. 왜 ‘+’가 사용되는걸까?
그 이유는 합성곱과 유사한 ‘교차상관’을 이용하기 때문이다. 사실 대부분의 CNN 알고리즘에서는 ‘합성곱’ 그 자체를 이용하지않는다. 왜냐면 filter를 학습시키는 것이 목적이기 때문이다. 만약 filter에 합성곱을 적용한다면 저 filter를 반전(뒤집기)시켜야 한다. 이는 불필요한 작업이다.
5. ReLU란? ‘활성화 함수’
예를들어 그런거다. 수학 시험에서 50점이 넘는 학생은 그 받은 점수를 그대로 내신에 반영하고 50점 이하인 학생들은 0점 처리를 한다고 해보자. 그럼 수학점수 56점, 70점, 80점, 62점 받은 학생들의 내신 점수는 각각 56, 70, 80, 62가 되는 것이고 25, 38, 44, 50 받은 학생들의 내신 점수는 모두 0점인 것이다.
ReLU도 비슷하다. x가 input이라고 해보자. x 값이 0 이하이면 f(x)=0 이고 x 값이 0보다 크면 f(x)=x인 함수가 ReLU이다. 이를 수식 및 그래프로 나타내면 다음 사진과 같다.
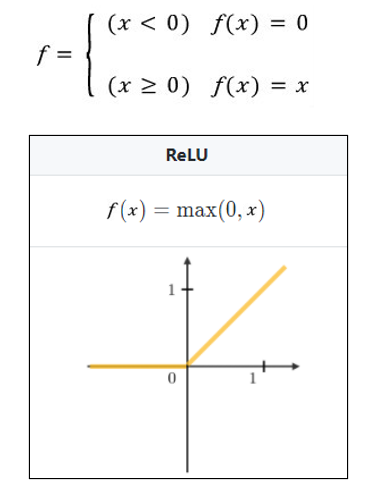
ReLU와 같은 함수를 ‘활성화 함수’라고 한다. 이러한 활성화 함수를 거치지 않은 노드의 상태는 보통 선형함수로 표현될 수 있다. 이 선형그래프를 비선형 형태로 바꾸는 역할을 하는 것이 이 ‘활성화 함수’이다. 불필요한 데이터 (위의 예에서는 50점 미만의 학생..)는 극소화 시키고 필요한 데이터를 추출하기 위해 필요하다.
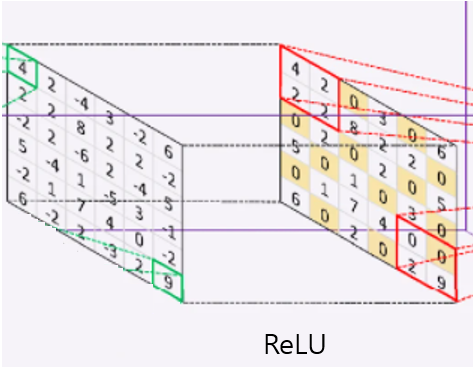
다음 사진은 ReLU를 통과시킨 노드이다. 0 혹은 음수값은 0으로 치환시키고 나머지 양수값은 그대로 가져가는 것을 확인할 수 있다.
6. Pooling이란?
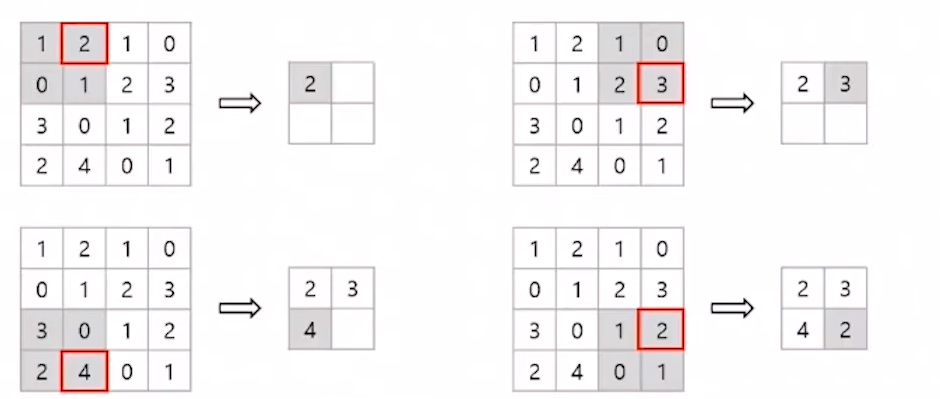
세로, 가로 방향의 공간을 줄이는 연산으로 Sub-sampling이라고도 한다. 쉽게 말하면 일정 영역을 선택해서 특정 값을 하나 가져오는 것이다. 다음 사진을 보면 이해가 쉽게 될 것이다.
Max pooling 방식은 해당 영역의 최대값을 가져오는 것이고 Average pooling 방식은 해당 영역의 평균 값을 가져오는 것이다. 다음 예제는 Max pooling 방식의 예이며 이미지 인식 분야에서는 주로 이를 사용한다.
7. Feature Learning 정리 (3~6 항목)
Feature Learning 단계의 내용을 정리하면 다음과 같다.
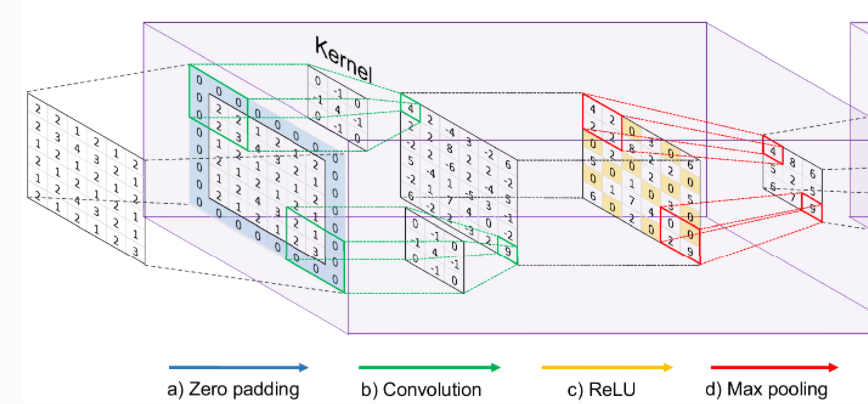
a. (언급한 단계는 아니지만) 합성곱 단계에서 노드가 지나치게 축소되는 것을 방지하기 위해 zero padding을 추가한다.
b. 합성곱 (정확히는 ‘교차상관’) 연산 단계이다. 여기서 Kernel을 통해 feature를 추출한다.
c. ReLU 함수를 통해 양수값을 제외하고 0으로 치환한다.
d. Max pooling 함수를 통해 각 대상영역(2x2)의 최대값을 뽑아온다.
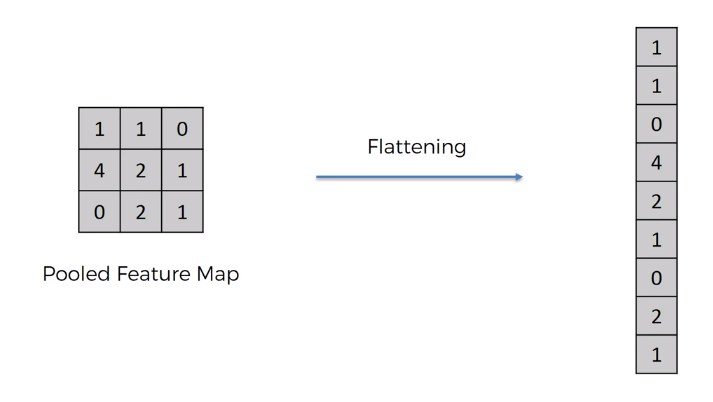
8. Flatten이란?
(a, b) 의 행렬로 구성된 데이터를 a x b 의 길이를 가지는 칼럼으로 바꾸는 작업을 의미한다. 이렇게 Flattening 된 행렬을 ReLU 함수를 거친 뒤 Softmax 함수의 input으로 전달한다.
Fully connected layer란 이렇게 1차원 배열의 형태로 평탄화된 행렬을 통해 이미지를 분류하는데 사용되는 계층이다.
9. Softmax 함수란?
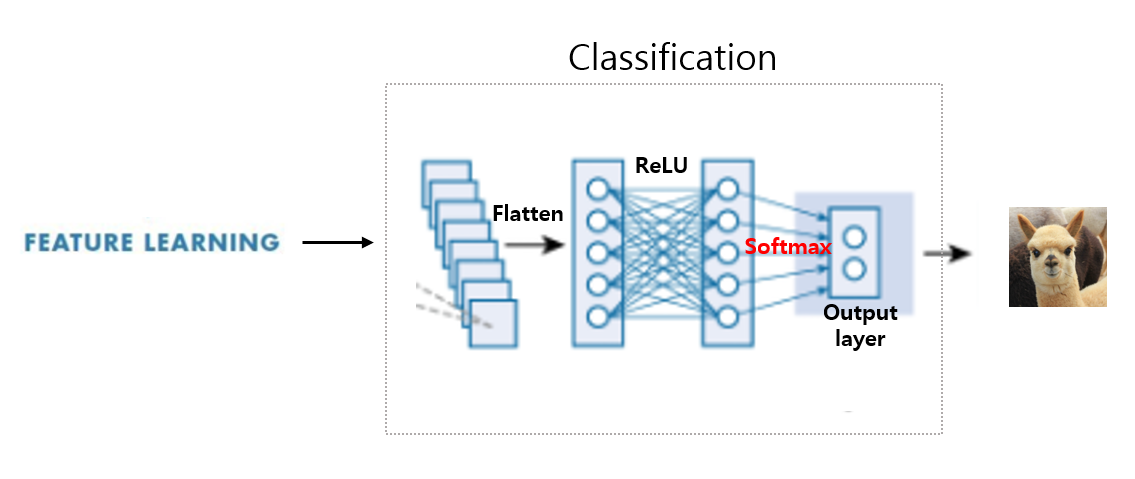
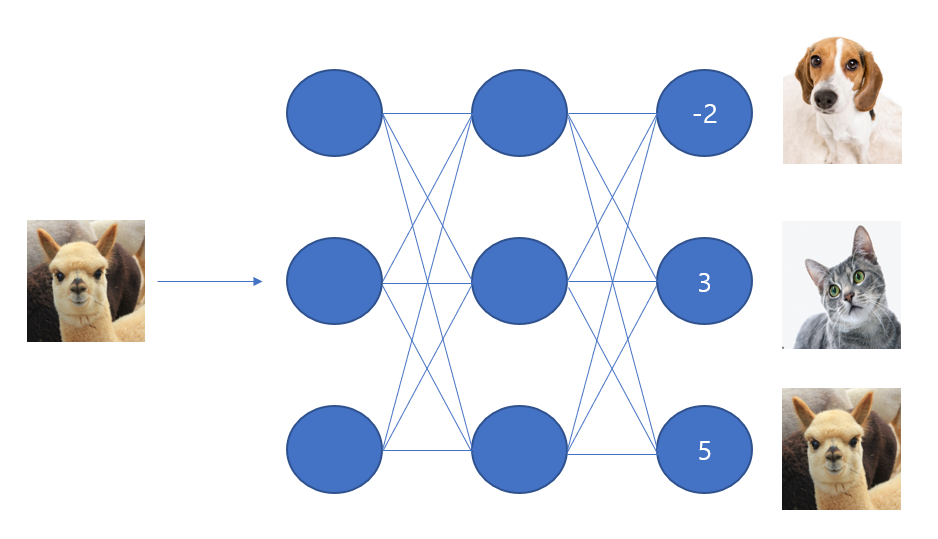
만약 Softmax라는 것이 사용되지 않는다면 상황은 다음 그림과 비슷할 것이다. 알파카 이미지의 input이 최종적으로 정수값으로 나오는 것을 볼 수 있다. 하지만 우리가 알고싶은 것은 ‘확률’이다. 이 확률을 계산하고자 Softmax 라는 활성화 함수가 사용된다.
공식은 다음 사진과 같다. 통계학에서 유명하기로 소문난 ‘로지스틱 함수’에서 비롯되었으며 해당 함수가 가진 특성인 이진분류의 한계점(참/거짓만을 판별)을 개선하여 나온 함수가 소프트맥스 함수이다. 공식을 보면 알겠지만 소프트맥스의 모든 항(a_0 ~ a_k)을 더하면 1이 나오는 구조로서 j항의 확률을 구할 수 있게 설계되어있다.
(언젠가 로지스틱 회귀 함수의 공식 유도과정을 작성해보아야겠다)
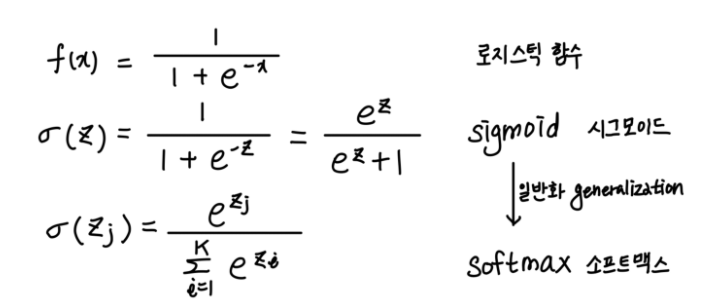
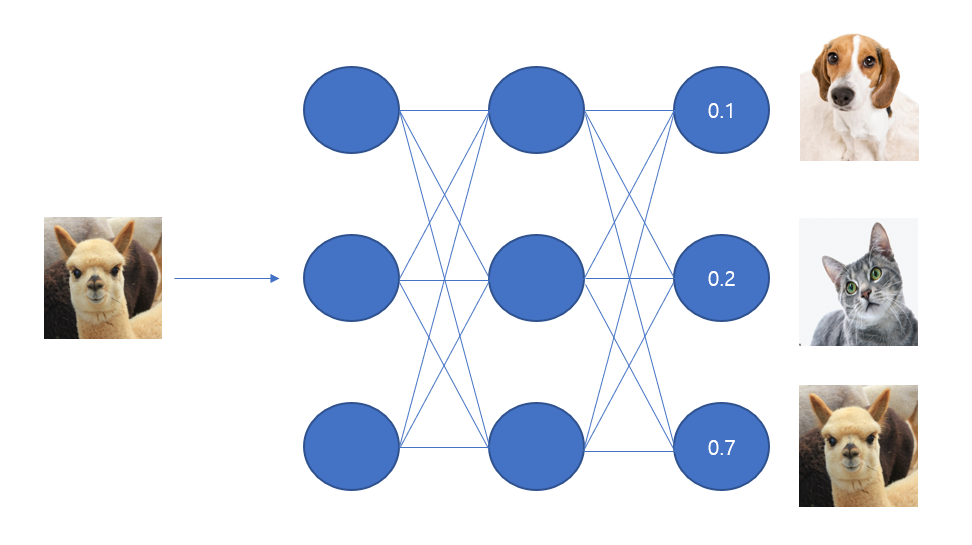
즉 소프트맥스 함수를 사용함으로써 다음 사진과 같이 전체 output의 값 중 확률적으로 최종값을 예측할 수 있는 것이다. 다음 예시는 알파카일 확률이 70%인 경우이다.
만약 소프트맥스가 아닌 로지스틱 함수를 사용하는 경우 0.3, 0,6, 0,8 과 같이 각 클래스의 총합이 1이 되는 것을 보장하지 않는다. 이것이 로지스틱 함수의 한계점이다.
10. Classification 정리 (8~9항목)
Flattening 되어 평탄화된 행렬을 ReLU, Softmax 함수를 거쳐 확률 형태로 output을 얻는 단계를 의미한다.